Page 1 of 1
Odd self intersection points
Posted: Wed Jun 16, 2021 10:24 pm
by CVH
Andrew,
How comes ...
Included a dxf with 2 polylines in different scales.
I marked the self-intersection vectors returned by:
var points = polyline.getSelfIntersectionPoints();
How comes that
.getSelfIntersectionPoints returns actual singular vertices of a polyline


First, presumed it was the minute scale of things, the smallest are actually 10x the originals.
Scaling up, there are even more singular vertices considered self-intersecting ...

Is there a function that can subtract a vertices array from the
.getSelfIntersectionPoints array?
Regards,
CVH
Re: Odd self intersection points
Posted: Thu Jun 17, 2021 4:56 pm
by andrew
This is very likely a tolerance issue (since there are arc segments involved). I will add a tolerance parameter for the next update.
Re: Odd self intersection points
Posted: Thu Jun 17, 2021 8:21 pm
by CVH
Ok, thanks.
Yes, bulging is involved as these are explosions of splines.
Snippets of the Eagle shape here:
https://qcad.org/rsforum/viewtopic.php? ... gle#p24417
Just any of the many shapes I use to lauch trial maths on.

- RoundCorners
- Pocketing
...
Regards,
CVH
Re: Odd self intersection points
Posted: Sat Jun 19, 2021 11:01 am
by CVH
Andrew,
https://github.com/qcad/qcad/commit/930 ... bb1274ddc9
For polylines form splines ... What are tangentially connected segments.
Catching almost all false positive nodes with 2e-8 tolerance ...

None with 1e-9 = RS.PointTolerance.
Depends a little on how far they sit from the origin >>> Larger 1ULP.
And on how good the polar representation of an arc endpoints can be.
While the Cartesian position changes, the bulging factor is equal and rather small here.
Another oddity is that nodes and endpoints of shapes from such a polyline
only differ in the range 3e-12 -- 5e-11

(node vs ends & end vs end)
Still, a tolerance gap of factor 2000 -10.000 ... One that I can't explain


Regards,
CVH
Re: Odd self intersection points
Posted: Sun Jul 18, 2021 11:23 am
by CVH
Andrew, All,
Based on a wide survey ... (0 ... 10,000,000)
Filtering all false positives from an
RPolyline.getSelfIntersectionPoints() list ...
Including for troublesome bulging polylines ...
Ignoring the bulge factors to arc shapes floating point uncertanties ...
But simply based on the largest absolute X or Y value of a box surrounding the polyline ...
Code: Select all
var box = entity.getBoundingBox();
var maxNumber = Math.max(Math.abs(box.c1.x), Math.abs(box.c1.y), Math.abs(box.c2.x), Math.abs(box.c2.y));
var tolerance = 4.00e-9 * Math.pow(maxNumber, 0.45);
Forgot a safety margin ...

This is based on the equation of a trend line of filtered results without false positives.
One may remark that:
- 4.00e-9 is 4x RS.PointTolerance.
- To power 0.45 is almost the root.
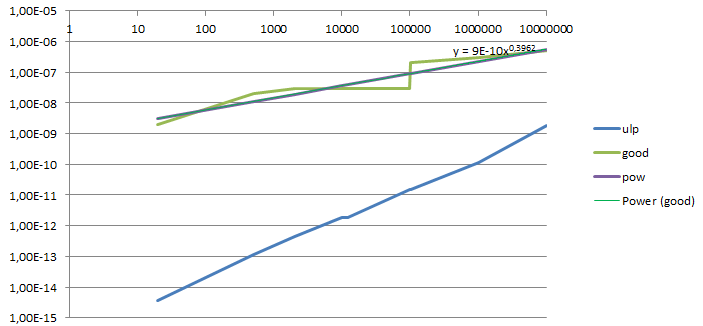
- Tolerance-Trend.png (12.03 KiB) Viewed 10498 times
Bottom line: The required tolerance value is governed by the Floating Point uncertainty of the coordinate values.
Regards,
CVH


