Making progress ...
As already pointed out in April, 2024, 17 months ago, in a comment on the bug report
FS#2565:
The a1<a2 branch has a non-strict inequality allowing for Pi.
Some non-strict inequalities should be implemented for the second branch.
In
REllipse::getLength():
For the second branch where
a1 is not strictly smaller than
a2 while they can't be equal at this point.
In essence meaning: Where
a1 is definitely larger than
a2.

Current
line 564 should read:
Also allowing that the end parameter angle
a2 is equal to Pi or 180°.
The returned length is then:
L(start..360) + L(0..end)
Current
line 567 remains AS IS:
Only the condition for
a2 is the opposite from the above.
Together they form the
a1>M_PI branch and can be simplified as such.
The returned length is then:
L(start..360) + half ellipse + L(180..end)

Current
line 570 should read:
Now the condition for
a1 is the opposite from the above two combinations, also allowing
a1 = Pi or 180°.
The condition for
a2 is strict because it must be smaller than
a1 even when
a1 is Pi.
Also ruling out the fourth combination of the 2 comparisons.
The returned length is then:
L(start..180) + half ellipse + L(0..end)

This would fix the problem of returning
NaN when none of the former 3 boolean combinations resolved to
true ...
... Returning at least a valid number value ...

However, the returned results are not so great in all cases.

- = - = - = - = 20 intervals is not the answer, it was an example = - = - = - = -
REllipse.getSimpsonLength(a1, a2) estimates the ellipse arc length based on the '
Composite Simpson's 1/3 rule'.
In the same article one can read how to
determine the number of intervals for a desired accuracy.
As per given example: 22 intervals for integrating
sin(x) from zero to Pi to within 1e-5 in absolute.
Other sources may also tend to promote a fixed number of 20 or so intervals in their examples.
The implementation in QCAD uses 20 intervals as in these examples.
Remark that this is only to keep the example simple.
Other examples exits, this
site uses the same technique with 1000 intervals but the accuracy is (very) limited.
- We are not integrating a simple sin(x) function.
Lower and upper bound are not zero and Pi per definition.
One can overdo it, attempting to chain-sum a vast amount of (much too) small values using floating point.
About 8 of 16 significant digits would be nice, the more the better.
...
..
.
Also, QCAD uses the same number of 20 intervals for estimating any ellipse arc up to 1/2 full ellipse.
Disregarding it is less than 0-Pi/2 or beyond.
Then an estimation for 0-Pi or Pi-2Pi uses much coarser intervals to integrate.
The result should not degenerate because of the case or because of adding a half ellipse length.
Turns out that the ideal number of intervals is highly exponential ...
To start with.
Similar to the eccentricity of an ellipse.
For integrating an ellipse arc from zero to Pi/2 its length, I came up with a rule of thumb that returns rather correct values:
- Even n intervals = 2 * floor(7.7 / ratio) where the ratio is the minor radius over the major radius.
A simplified version of the function for a fitted curve on a list of almost ideal numbers of intervals vs ratios.
For a ratio of 0.75 or over the number of intervals would be 20 and as low as 14.
What is fine for the orbit of planets in a solar system for example ... The major field of interest ...
... We tend to draw different kinds of ellipses.
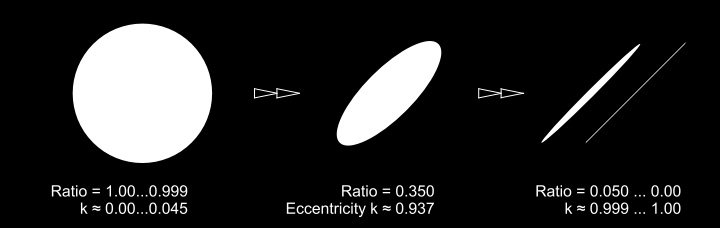
- EllipseRatiosEccs.png (18.08 KiB) Viewed 21482 times
- Ratio = 0.50 >> 30 intervals.
Ratio = 0.35 >> 44 intervals.
Ratio = 0.20 >> 76 intervals.
Ratio = 0.10 >> 154 intervals.
Ratio = 0.05 >> 308 intervals.
Ratio = 0.01 >> 1054 intervals.
Beyond that the ellipse starts to look more like a line going back and forth.
Hits and misses: 
A) While the rule of thumb is '
the solution' for estimating the length of a quarter, a half or a full ellipse very precise.
It doesn't holds for estimating the length of an arbitrary ellipse arc.
The number of intervals doesn't decrease, it get bigger, unpredictable bigger.
B) Beyond a few hundreds or so intervals, the computational effort is simply too large, especially if this concerns an entity property.

The only solution I see is to implement elliptic integrals of the first and second kind as I did.
Coding the Math in not that hard and it is not really demanding compared with 2-3 calls to the
REllipse.getSimpsonLength(a1, a2) function
Limited to 20 intervals itself already:
21 cosine, 21 sine, 21 square root, 42 squares, 19 modulo operation, 2 divisions, 106 multiplications, 84 addition/subtractions, 40 if-else, 61 comparisons, 87 assignments
An example can be found in the old but legendary Cephes Math Library, available under a '3-clause BSD license'.
Phyton SciPy and others includes this just the same, also see
https://www.npmjs.com/package/cephes.
Translation to JS under QCAD posed some unexpected and hard to figure out specialties ...

It was very instructive to see how badly things go for ellipse eccentricities from 0.66 up to 1.0 or ratios below 0.75 and towards zero.
Regards,
CVH